Matriks dalam Bahasa Indonesia

Matriks merupakan salah satu konsep penting dalam matematika. Matriks adalah susunan bilangan dalam bentuk baris dan kolom yang membentuk suatu persegi panjang. Setiap elemen dalam matriks memiliki posisi yang ditentukan oleh baris dan kolomnya. Dalam artikel ini, kita akan membahas lebih lanjut mengenai matriks beserta aplikasinya dalam berbagai bidang.

Pengertian Matriks

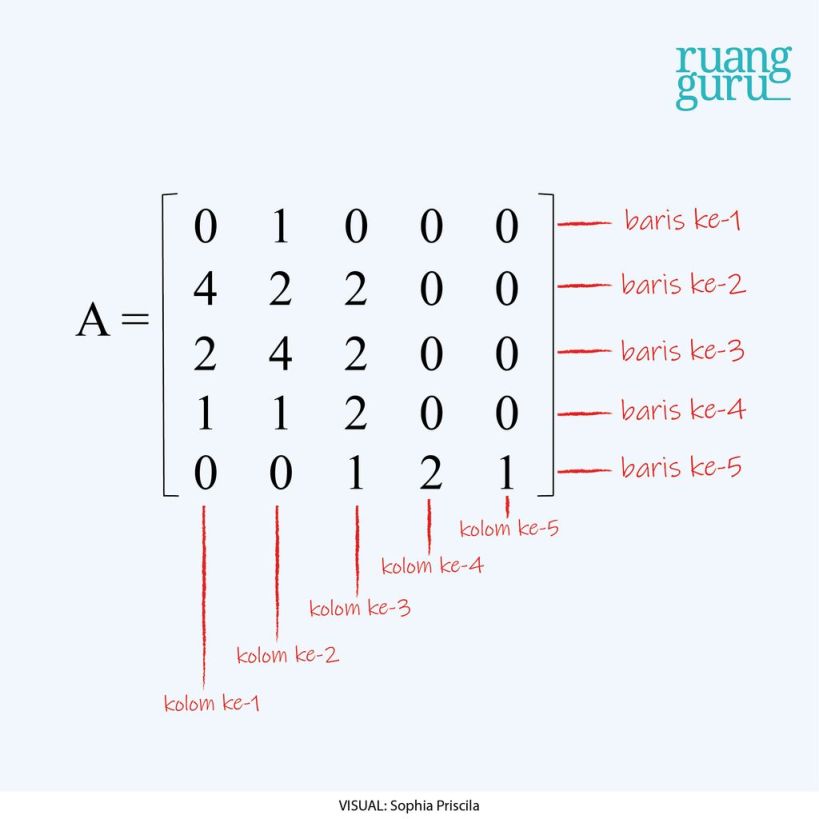
Matriks adalah suatu struktur data yang terdiri dari bilangan-bilangan yang disusun dalam bentuk baris dan kolom. Setiap elemen dalam matriks dapat diidentifikasi berdasarkan posisi baris dan kolomnya. Misalnya, matriks A dengan ukuran m x n memiliki m baris dan n kolom, sehingga matriks A dapat ditulis sebagai:

[a11 a12 a13 … a1n]

[a21 a22 a23 … a2n]

[a31 a32 a33 … a3n]

[… … … … …]

[am1 am2 am3 … amn]

Dalam contoh di atas, aij merupakan elemen matriks A yang terletak pada baris ke-i dan kolom ke-j.

Jenis-Jenis Matriks

Ada beberapa jenis matriks yang sering digunakan, antara lain:

1. Matriks Nol: Matriks yang semua elemennya bernilai nol.

2. Matriks Identitas: Matriks persegi yang memiliki nilai 1 pada diagonal utamanya dan 0 pada elemen-elemen lainnya.

3. Matriks Baris: Matriks dengan hanya memiliki satu baris.

4. Matriks Kolom: Matriks dengan hanya memiliki satu kolom.

5. Matriks Segitiga Atas: Matriks dengan elemen-elemen di bawah diagonal utama bernilai nol.

6. Matriks Segitiga Bawah: Matriks dengan elemen-elemen di atas diagonal utama bernilai nol.

7. Matriks Persegi: Matriks yang memiliki jumlah baris dan kolom yang sama.

Operasi Matriks

Operasi matriks melibatkan manipulasi terhadap matriks-matriks yang ada. Beberapa operasi matriks yang sering dilakukan antara lain:

1. Penjumlahan dan Pengurangan Matriks: Elemen-elemen matriks yang posisinya sama saling ditambah atau dikurangi.

2. Perkalian Matriks: Mengalikan setiap elemen matriks dengan elemen yang berada pada posisi yang sama pada matriks lainnya.

3. Transpose Matriks: Menukar posisi baris menjadi kolom dan sebaliknya.

4. Determinan Matriks: Nilai yang diperoleh dari operasi matematika tertentu terhadap matriks.

5. Invers Matriks: Matriks yang apabila dikalikan dengan matriks asal menghasilkan matriks identitas.

Aplikasi Matriks

Matriks memiliki berbagai aplikasi dalam berbagai bidang, di antaranya:

1. Grafika Komputer: Matriks digunakan untuk menggambarkan objek dalam ruang tiga dimensi.

2. Ekonomi: Matriks digunakan untuk menganalisis hubungan antara variabel-variabel ekonomi.

3. Fisika: Matriks digunakan dalam perhitungan fisika kuantum dan mekanika klasik.

4. Teknik Mesin: Matriks digunakan dalam perancangan struktur dan sistem kontrol.

5. Statistik: Matriks digunakan untuk analisis data dan peramalan.

Kesimpulan

Matriks adalah struktur data yang terdiri dari bilangan-bilangan yang disusun dalam bentuk baris dan kolom. Matriks memiliki berbagai jenis dan dapat digunakan dalam berbagai bidang, seperti grafika komputer, ekonomi, fisika, teknik mesin, dan statistik. Operasi matriks seperti penjumlahan, perkalian, transpose, determinan, dan invers juga sering dilakukan. Dengan pemahaman yang baik tentang matriks, Anda dapat mengaplikasikannya dalam pemecahan masalah dan analisis data.

FAQ

1. Apa beda matriks baris dan matriks kolom?

Matriks baris hanya memiliki satu baris, sedangkan matriks kolom hanya memiliki satu kolom.

2. Apa itu matriks identitas?

Matriks identitas adalah matriks persegi yang memiliki nilai 1 pada diagonal utamanya dan 0 pada elemen-elemen lainnya.

3. Apa itu transpose matriks?

Transpose matriks adalah operasi menukar posisi baris menjadi kolom dan sebaliknya.

4. Apa itu determinan matriks?

Determinan matriks adalah nilai yang diperoleh dari operasi matematika tertentu terhadap matriks.

5. Mengapa matriks digunakan dalam analisis data?

Matriks digunakan dalam analisis data karena dapat merepresentasikan hubungan antara variabel-variabel data secara komprehensif dan melakukan operasi matematika yang relevan.