Daftar Isi

Himpunan

Definisi Himpunan

Himpunan adalah konsep dasar dalam matematika yang digunakan untuk mengumpulkan objek-objek dengan karakteristik yang sama. Objek-objek tersebut bisa berupa angka, huruf, kata-kata, atau bahkan objek-objek lainnya. Dalam matematika, himpunan sering digunakan untuk menganalisis dan mengklasifikasikan objek-objek tersebut.

Elemen dalam Himpunan

Setiap objek yang termasuk dalam suatu himpunan disebut sebagai elemen. Elemen-elemen ini bisa berupa angka, huruf, atau objek-objek lainnya. Misalnya, dalam himpunan angka bulat positif kurang dari 10, elemen-elemennya adalah angka 1, 2, 3, 4, 5, 6, 7, 8, dan 9.

Notasi Himpunan

Notasi yang digunakan untuk menyatakan himpunan adalah dengan menggunakan tanda kurung kurawal {}. Misalnya, himpunan angka bulat positif kurang dari 10 dapat ditulis sebagai {1, 2, 3, 4, 5, 6, 7, 8, 9}. Jika sebuah elemen termasuk dalam suatu himpunan, maka elemen tersebut ditulis di dalam kurung kurawal. Jika tidak termasuk, maka elemen tersebut tidak ditulis.

Macam-macam Himpunan

Ada beberapa jenis himpunan yang sering digunakan dalam matematika, antara lain:

1. Himpunan kosong: himpunan yang tidak memiliki elemen, biasanya ditulis sebagai ∅.

2. Himpunan satu elemen: himpunan yang hanya memiliki satu elemen, misalnya {2}.

3. Himpunan universal: himpunan yang berisi semua elemen yang dibahas dalam suatu konteks tertentu. Misalnya, himpunan angka bulat positif kurang dari 10 adalah himpunan universal dalam contoh sebelumnya.

4. Himpunan terbatas: himpunan yang memiliki jumlah elemen yang terbatas. Misalnya, himpunan angka bulat positif kurang dari 5 {1, 2, 3, 4} adalah himpunan terbatas.

5. Himpunan tak terbatas: himpunan yang memiliki jumlah elemen yang tidak terbatas. Misalnya, himpunan bilangan bulat positif {1, 2, 3, 4, …} adalah himpunan tak terbatas.

Operasi Himpunan

Dalam matematika, terdapat beberapa operasi yang dapat dilakukan pada himpunan, antara lain:

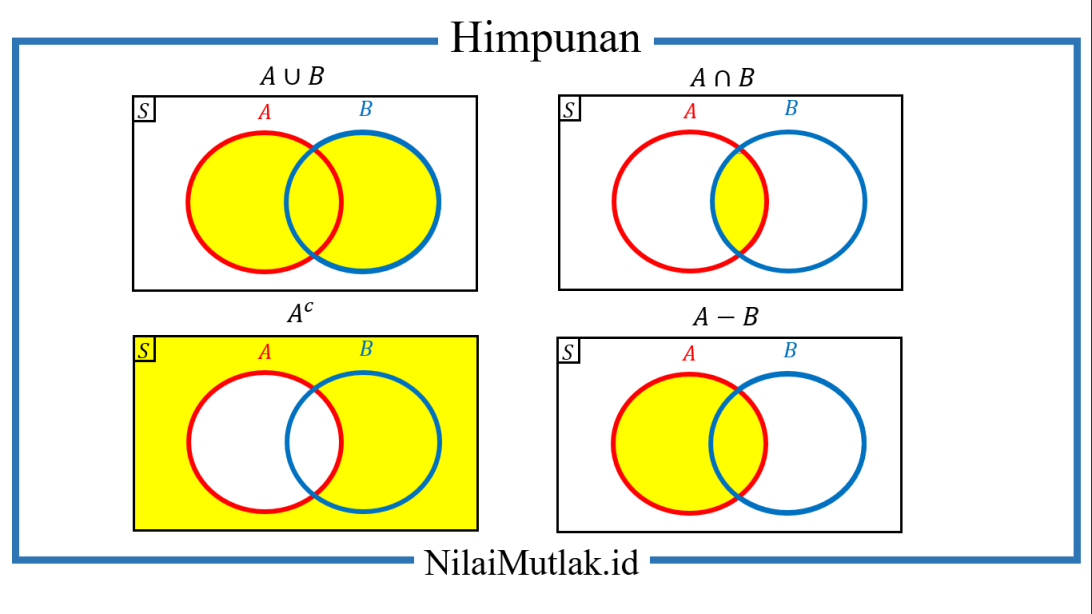
1. Gabungan (union): operasi untuk menggabungkan dua himpunan menjadi satu himpunan baru. Simbol yang digunakan adalah ∪. Misalnya, jika A = {1, 2, 3} dan B = {3, 4, 5}, maka A ∪ B = {1, 2, 3, 4, 5}.

2. Irisan (intersection): operasi untuk mencari elemen-elemen yang sama dalam dua himpunan. Simbol yang digunakan adalah ∩. Misalnya, jika A = {1, 2, 3} dan B = {3, 4, 5}, maka A ∩ B = {3}.

3. Selisih (difference): operasi untuk mencari elemen-elemen yang ada di himpunan pertama tetapi tidak ada di himpunan kedua. Simbol yang digunakan adalah . Misalnya, jika A = {1, 2, 3} dan B = {3, 4, 5}, maka A B = {1, 2}.

4. Komplement (complement): operasi untuk mencari elemen-elemen yang tidak termasuk dalam himpunan. Simbol yang digunakan adalah ’. Misalnya, jika A = {1, 2, 3} dan U adalah himpunan universal, maka A’ = {4, 5, 6, …}.

Penerapan Himpunan dalam Kehidupan Sehari-hari

Konsep himpunan sering digunakan dalam kehidupan sehari-hari. Misalnya, dalam memilih baju untuk dipakai, kita dapat mengelompokkan pakaian-pakaian tersebut ke dalam himpunan pakaian formal, pakaian kasual, atau pakaian olahraga. Dalam memilih menu makanan, kita dapat mengelompokkan makanan-makanan tersebut ke dalam himpunan makanan pedas, makanan manis, atau makanan sehat.

Selain itu, dalam dunia bisnis, himpunan juga digunakan untuk mengelompokkan pelanggan berdasarkan kriteria tertentu, seperti usia, jenis kelamin, atau preferensi produk. Dengan menggunakan konsep himpunan, informasi tentang pelanggan dapat dianalisis dengan lebih mudah dan efisien.

Kesimpulan

Dalam matematika, himpunan adalah konsep dasar yang digunakan untuk mengumpulkan objek-objek dengan karakteristik yang sama. Elemen-elemen dalam himpunan bisa berupa angka, huruf, atau objek-objek lainnya. Terdapat beberapa jenis himpunan dan operasi yang dapat dilakukan, seperti gabungan, irisan, selisih, dan komplement. Konsep himpunan juga memiliki penerapan dalam kehidupan sehari-hari, baik dalam pemilihan pakaian, makanan, maupun dalam analisis bisnis.

FAQ tentang Himpunan

1. Apa itu himpunan kosong?

Himpunan kosong adalah himpunan yang tidak memiliki elemen. Biasanya ditulis sebagai ∅.

2. Apa perbedaan antara himpunan satu elemen dan himpunan kosong?

Himpunan satu elemen adalah himpunan yang hanya memiliki satu elemen, sedangkan himpunan kosong tidak memiliki elemen sama sekali.

3. Apa itu himpunan universal?

Himpunan universal adalah himpunan yang berisi semua elemen yang dibahas dalam suatu konteks tertentu. Misalnya, himpunan angka bulat positif kurang dari 10 adalah himpunan universal dalam contoh sebelumnya.

4. Apa itu operasi gabungan dalam himpunan?

Operasi gabungan dalam himpunan adalah operasi untuk menggabungkan dua himpunan menjadi satu himpunan baru. Simbol yang digunakan adalah ∪.

5. Bagaimana penerapan himpunan dalam bisnis?

Himpunan digunakan dalam bisnis untuk mengelompokkan pelanggan berdasarkan kriteria tertentu, seperti usia, jenis kelamin, atau preferensi produk. Dengan menggunakan konsep himpunan, informasi tentang pelanggan dapat dianalisis dengan lebih mudah dan efisien.